Del siglo de oro de Pericles a la síntesis digital de bajos recursos

Heidegger, agregando dramatismo filológico con mucha creatividad a lo que había ya dicho Nietzsche, sostenía que en la Antigua Grecia del siglo IV a.C., la techne había alcanzado un grado de desarrollo inusitado en relación a lo que todavía hoy, disimuladamente, secularmente, podría admitirse como lo bello (esta coincidencia en el valor ontológico del hacer lo animó a pseudosemidesnazificarse al proponer insólitamente un diálogo con el marxismo en su “Carta sobre el humanismo” de 1947). Nietzsche creía que la ciencia y la filosofía eran expresiones decadentes de una sociedad cuyo máximo prodigio fueron las artes, y más concretamente la tragedia. Por eso un poco precipitadamente hablamos de rupturas o vanguardias, ya que por entonces se llegó a vivir un ritmo tan acelerado de innovaciones y escándalos estéticos que explican la posición conservadora de Platón para la proyección de una transformación social (algo que era cosustancial a la disciplina espartana pero que el cristianismo tuvo que imponer con terror, de forma cada vez más alarmantemente comparable a las moralinas contemporáneas). La experimentación y discusión sobre los límites y el sentido de lo sonoro, felizmente, tiene lugar entre nosotros pero es – como diría Borges, según lo propio de la eternidad – una adivinanza lo mismo que una predicción.

La escuela pitagórica se imponía con su metafísica matemática y por eso no era sorprendente (y tampoco sorprende hoy) que muchos proclamados teóricos musicales no hablaran más que de fórmulas y geometrías, como si cualquier experiencia de la vida sensible fuera una posible excusa para realzar su ontología de magnitudes cuantitativas. Contra esta concepción escribió Aristóxeno de Tarento (354-300 a.C.) uno de los tratados más influyentes y a la vez ignorados de la conceptualización del lenguaje musical. Aristóxeno sostenía que la música era, ante todo, un fenómeno estético, sensorial, y que como fenómeno físico podía estudiarse matemáticamente pero su cualidad estaba principalmente determinada en la subjetividad que agrupaba las excitaciones del cuerpo en una unidad de sentido, en un discurso, en un acontecimiento temporal, sensual, que los pitagóricos transustanciaban al abstraer la experiencia concreta de la escucha.

Dicho esto tengo que advertir que, por cuestiones de interés práctico más que filosóficas, voy a referirme, irónicamente, a cuestiones pitagóricas más que estéticas de cómo encuentro satisfacción en el desarrollo de un lenguaje de improvisación porque consiste básicamente en la complejización de una función matemática. La poiesis inspirada y regulada de la evolución de esta función pertenece al campo de la escucha en un sentido profundo y, por lo tanto, exige un tratamiento filosófico que, por el momento, voy a suspender.

Hace casi veinte años que programo en Pure Data y muchos más de veinte desde que me enamoré de las computadoras en un vínculo lúdico y estético (lejos de las bases de datos que eran lo único monetizable por entonces). Antes de saber que ya existía un nombre para describir esta práctica específica, comencé con mi hermano a programar en vivo, mostrando el código de manera espontánea, como quien lanza una botella con un mensaje desde una isla desierta o viste una remera de su banda favorita esperando encontrar cómplices de su placer perdidos en el barroco y corroído paisaje urbano falto de experiencias, como diría Agamben.

Pure Data es un lenguaje modular de procesamiento de señales digitales en tiempo real, esto lo vuelve instintivo e inagotable en términos de síntesis pero también se me hacía extremadamente incómodo y engorroso improvisar. Conforme dirigía mi práctica más y más a la improvisación de código, buscaba la combinación más pequeña y sencilla de módulos-objetos que a la vez no fuera en detrimento de las posibilidades de procesamiento. Reducía cada vez más las conexiones y los esquemas hasta que una vez me puse una especie de consigna imposible: tengo que lograr hacer todo con un solo oscilador. Un día, hará dos o tres años – creo que fue saliendo de un CASo Abierto –, Hernán Kerlleñevich me sugirió que busque información sobre “bytebeat”.

Bytebeat es el nombre de una técnica de síntesis digital de bajos recursos, cuyo precursor describió sin más como “descubrimiento”. Aunque se activan algunas alarmas conceptuales al referirse a una fórmula como descubrimiento, cada vez me parece más simpática esta inocente caracterización. Porque los recursos para esta técnica están disponibles desde hace muchísimo tiempo (de hecho, la principal inspiración parece que fue una demo de Commodore VIC-20) y, sin embargo, no fue hasta que tuvimos procesadores tan exagerados, en relación a lo que es más que suficiente para hacer bytebeat, que finalmente alguien lo investigó y desarrolló más detalladamente.

Me gusta entender al bytebeat con ese destello estético que aparece en el ámbito de la ciencia: la elegancia. Se considera elegante a una fórmula que de la manera más simple y económica satisface los resultados más extensos y complejos. La técnica bytebeat consiste en escribir una función lógico-matemática, por lo general de escasos caracteres, con operaciones de bajo nivel, que tome como única variable el tiempo y mandar el resultado de esta operación “en crudo” al conversor analógico digital, la salida de audio. Para dar una idea, el código o “partitura” de una obra generativa de varios compases de extensión clásica del bytebeat es literalmente:

((t >> 10) & 42) * t

La variable “t” es tiempo, concretamente se trata de un contador regular, un número que incrementa rápidamente en intervalos de unidad equidistantes en el tiempo, una rampa o cronómetro. En una analogía válida podríamos decir que “t” es un LFO diente de sierra de mucha amplitud y nuestra fórmula es un wave-shapper de esa señal. En realidad, “t” es algo más cercano a un contador de samples. Podríamos hacer coincidir la rampa con el sample rate, la “resolución digital X”, o sea, +44100 por segundo. Entonces, el resultado en cada momento de nuestra función determina el valor de cada sample. Es decir, potencialmente se puede crear cualquier sonido dentro de las posibilidades de procesamiento digital. Sin embargo, para esto consideré necesario introducir una modificación en el algoritmo del bytebeat. ¿Por qué?

El bytebeat fue concebido de manera tal que cualquier resultado de la fórmula se escale, se mapee, a un número válido, a un valor existente dentro del espectro del bit depth, de la “resolución digital Y” del sonido. De esta manera no hay “error” posible en la fórmula, es decir, más allá de si produce un efecto deseado, ningún resultado excederá los límites de la señal sonora. Esto produce, además, un comportamiento que muchos no dudan en clasificar como fractal. Los “errores” de la función son reincorporados de alguna manera siempre a los valores posibles, generando simetrías (pido disculpas por la precariedad, reducción e imprecisión de mi lenguaje en estas cuestiones, habrán notado que al descartar un desarrollo filosófico opté por el camino más difícil para mí pero estos conocimientos me parecen demasiado valiosos como para no difundirlos). El problema es que al escalar todos los valores perdemos la posibilidad, por ejemplo, de manipular la amplitud de un modo sencillo. Veamos…

Suponiendo que estamos trabajando con una resolución de 8 bits (1 byte), el resultado de nuestra función será escalado mediante %255 a uno de los 256 valores posibles de amplitud (el 0 se cuenta). Si la función devuelve un número más grande o más pequeño, por ejemplo 260, el módulo (%) convierte al excedente en el valor final: 4. Pero supongamos que quiero generar una onda cuadrada t%2 y reducir su amplitud a la mitad multiplicando o dividiendo como (t%2)*0.5 o (t%2)/2, esto tendría otras consecuencias, no en la amplitud sino en la frecuencia. Lo que hice yo, entonces, fue quitar este mapeo a valores posibles y dejar únicamente un limitador, perdiendo esa natural fractalidad del bytebeat pero ganando en resolución, modelado y legibilidad. También es importante destacar que el objeto que en Pure Data permite procesar estas expresiones (expr~), también admite muchas más operaciones como, por ejemplo, funciones trigonométricas.

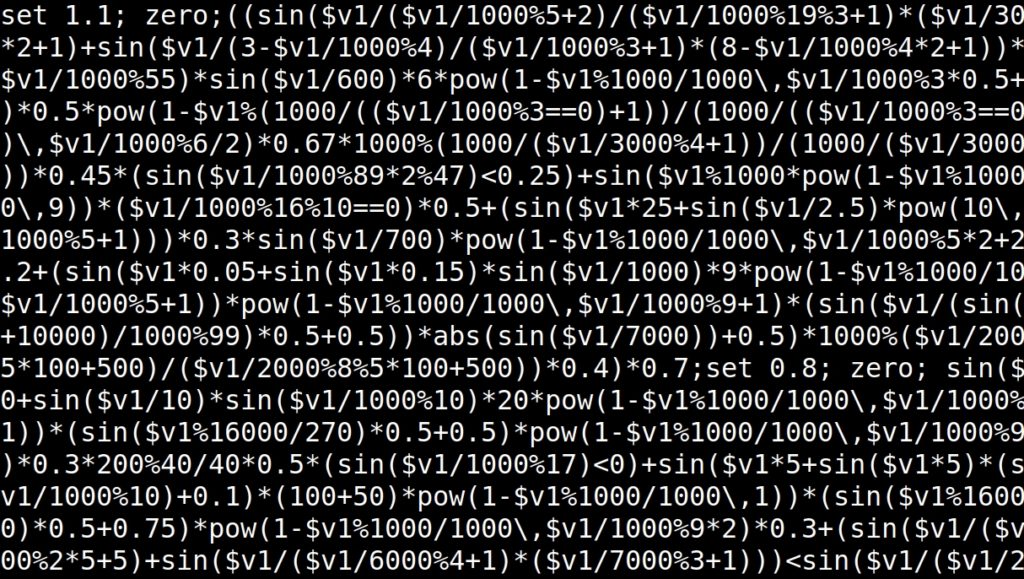
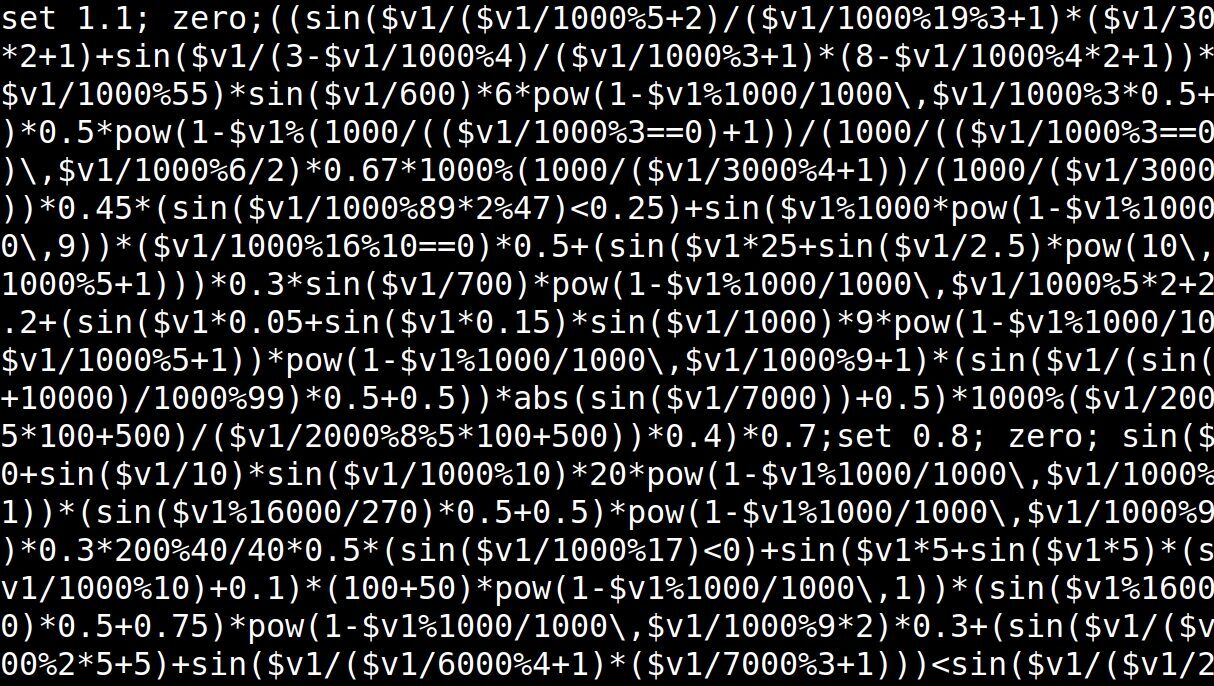
El sistema que armé, y en el que sigo trabajando constantemente, se llama Rampcode y gracias a la colaboración de Reo Matsumoto existe un paquete para utilizarlo con Atom editor. Recientemente incorporé la posibilidad de reemplazar la variable por otra (a la vez función de la primera), agregando una función en el medio. Así que, una vez que tengo algo sonando que me gusta o que tiene “momentos” que me gustan, puedo alterar su secuenciación y velocidad modificando la función anterior, obteniendo variaciones y “efectos”.

Rampa → Función (por defecto = Rampa) → Función

Para ver – y escuchar – más en detalle todas estas cuestiones dejo una selección de links un poco ecléctica, como este discurrir. Queda pendiente, para pronto o quizás nunca, un desarrollo más filosófico respecto de la experiencia estética, seguramente afirmando el plano de inmanencia del lenguaje, en un tono menos pitagórico, con las notas más bellas que me sean posibles.

https://greggman.com/downloads/examples/html5bytebeat/html5bytebeat.html

Un entorno de bytebeat online para jugar un poco.

http://pelulamu.net/ibniz/

En mi opinión, el mejor software de bytebeat.

http://viznut.fi/en/

El pionero del bytebeat y otras genialidades.

http://www.biblioteca.unlpam.edu.ar/pubpdf/circe/v4a09cotello.pdf

Un artículo de respetable academicidad que encontré en castellano sobre Aristóxeno (ver p.162).

https://github.com/gabochi/rampcode

El repositorio de Rampcode.